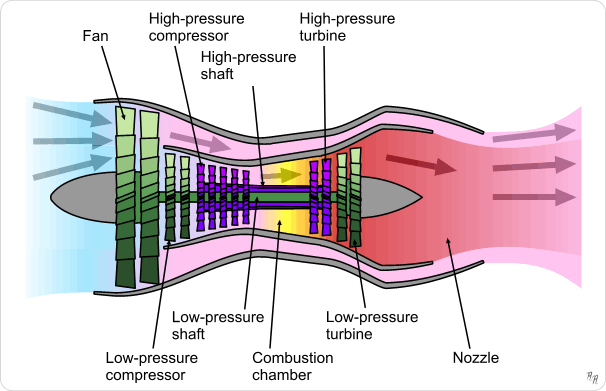
Turbofan remaining useful life Prediction
19.07.2019
In diesem Jupyter Notebook untersuchen wir, welche Ursachen für einen Fehler in der Hochdruckkompressoreinheit (HPC) eines Flugantriebsmotors verantwortlich sind. Darüber hinaus verwenden wir verschiedene Sensoren, um die verbleibende Nutzungsdauer (remaining useful life RUL) vorherzusagen.
